For a long time, I really didn’t get to treat this blog as my own blog. I mean, sure, I said things I’m enthusiastic about. But I think the purpose of having a blog is not about catching attention rather having a safe place where you can have a dialogue with your mind.

I recently started dabbling with functional programming. I don’t know why though. For long I heard a lot over it from the constant stream of social networks. I never managed to find a reason why should I ever care about this. I think secretly I was afraid if I ever take this up, I might succumb to my curiosity and finally spend time learning things I really don’t need right now. Then again, knowledge never fails.

So, here I am. After spending around 8 or 9 hours of active reading, I barely made a scratch in the surface of it. But it’s a start. My major breakthrough was to be able to get back to that mindset where I could just play with something when I have the least knowledge backing it. It’s a scary game but boy is this fun to play.

 

Ahoy! functional programming!

The first and foremost notion of functional programming I got from watching people talk about it is that it probably has something to do with ‘functions’ being the first citizen in a programming language. And immutability plays a big part. That lead me to the same place where I started learning programming.  I mean I knew “what” was I learning, I did not know “why” I was learning that. I didn’t have the guts to ask because I didn’t know anything about the context. Now, I stand in a corner where I get to ask the question. Why?

 

Why functional programming is like this?

Surprisingly functional programming didn’t spawn from the concept of programming construct “function” being the first class citizen in a programming language. The fun thing is the word ‘functional’ in the very title doesn’t even point to programming functions. It actually points to mathematical functions. Before I go into that, please allow me to tell yourself to ‘unlearn’ programming as you know it. Especially if you are a person like me who knows imperative programming only.  The reason to unlearn what you know is to give you a clean fresh slate to work with. I know that is easier said than done. But as long as you know it and open to see things, you’d be fine!

So, let’s dive in. Let’s assume a simple, very simple mathematical function like the following:

let add1 x = x + 1

For reference I’m using F# here. The two programming languages I want to at least try out is F# and Scala. There’s a solid debate on Scala not being a total functional programming language. But, that is a story for another day. My goal is to understand Apache Spark better in the process too and Scala is just too friendly with it. In the process I’m trying to kill two birds with one bullet. This blog will roughly use F# for reference but nothing here is not understandable even if you haven’t seen F# in your life.

If we have a look at the function here we will see that we are adding 1 to another number here. Any programming language in existence is capable of doing that. What is the difference here except the syntax? This is where I send you back to the “unlearn” step. Let’s see how this is interpreted inside. The F# interpreter will read the function signature like the following:

val add1 : x:int -> int

the  val add1 part is self explanatory, we don’t want to worry about that part right now. What about the next part x:int -> int. This is where my imperative programming brain came into work and devised a misleading explanation. And it sounded something like :

The x:int -> int stands for a method signature that takes an input parameter x of type int and it returns another int.

Like I said, this is wrong but it felt legit when I devised it in my brain. The more I delved into it, the more I realized the wrongs in my ways. Years of imperative programming have assembled my neurons to reinforce these concepts as the general means of programming. Since functional programming resorts to mathematical functions, why can’t we see it from that specific aspect?

A mathematical function takes a set of values that are used as inputs into the function domain and the function maps it to a set of possible outputs. The set of the outputs are called range. All the functions do here is map the inputs to the outputs.

To visualize:

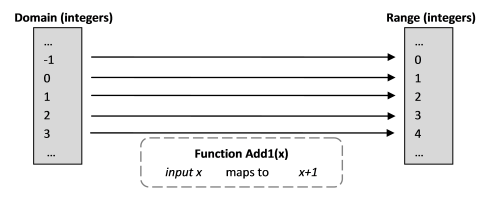
I’m not sure whether I have explained enough how my brain was convinced that it is different. To reinforce that the biggest difference here to look for is the process of doing things. We are transforming the inputs here. Not necessarily returning a value. Mathematical functions transforms inputs, they don’t produce any  side effect to the inputs. What I want to mean is if you add 5 and 1 you will get back 6. The input parameter 5 will not have any possible side effect on it. And a mathematical function always gives the same output for a specific given input. My imperative programming brain got it almost right. The right explanation for  x:int -> int is an int domain to int range mapping.

The function add1 maps an int input domain to an int range. And for the fact that mathematical functions DO NOT implicate any side effects, it was implicitly important to have immutability embedded inside them. Because if your programming function generates a state or a side effect then it will  not comply with mathematical functions. So the implementation layer will fail to comply with the theoretical counterpart. And that is why immutability is vital in functional programming.

 

I still don’t see the difference

This is really nice and all. But from my imperative programmer brain’s perspective, is it really that different? If I didn’t take this journey to figure out why functional programming is like this, won’t I be able to write anything in any possible functional programming language? And yes, for sure my brain will be able to. But here is the fun part. What our brain learns implicitly is really hard to explain using the same brain. Otherwise, machine learning will be a piece of cake. My point was to actually try to “know” it, not get habituated to it. Thus when I encounter a problem I can deduce a solution through what I know rather than just plugging constructs I have seen.

Still, I need an answer. Where is the difference? I still see inputs and outputs. Nothing else. My imperative programmer brain is quite right here, we assign a value to a variable and the function returns a result. 

Now, wait a minute and lets see a bit into the word variable and assign. The word variable and assign points to the fact where we use the variable as a placeholder for the actual value . And the concept of assigning a value to a variable points to the concept of storing something in that placeholder. Is it the same here? No. Mathematical methods don’t imply placeholders. It creates a mapping and generalizes that mapping. So saying add1 5 is not assigning 5 to x. It is actually binding 5 to x. The process of binding is not reusing add1. add1 5 is pointing to a method binding that says when I’m invoked you will end up in the range.  It looks really the same but it is not. Think of basically doing a string replace where the x is replaced with 5.

Hopefully now you will see more reasons reinforcing immutability. And thus the function name,  add1 is not a reusable construct for the function. It’s just a shortcut expression for the range it returns. We are replacing a function value, not the function!

To sum it up the generic function value signature is 

val functionName : domain -> range

So, here’s a trick question. How do we define constants then? The answer is writing a function where the range is just the value from any possible domain. 🙂

The motivation behind starting to write again while I learn something goes straight to Chris Smith. He wrote Programming F# and his MSDN blog while he was writing F# is found here. They are highly entertaining and please don’t refrain yourself from looking into them. According to him it is one of the best ways to learn a language and I kind of agree with him despite the fact I lost the courage or interest to do that regularly before.

I also found Learn X in Y Minutes very very fun to have a blind date with a number of programming languages. If I ever get to talk about Scala (that depends on me having time to learn it), I will definitely talk more about this website.

The resources for this blog are taken from:

1. F# for fun and profit
2. Learn X in Y Minutes

Hope this was entertaining albeit it comprises of boring details! I intend to write a dummies note onthe church-turing hypothesis which essentially blossomed into lambda calculus. Functional Programming is almost directly derived from it. But, it all depends on how much time I will possibly have to cover that. Until then, see ya.